
THE THEORY OF GUIDED BEAMS,
A short history
1959 Vlasov,V. Z.: Tonkostennye uprugie sterzhni (Thin-
Walled Elastic beams)
* the theory of sectorial areas and bimoment torsion of open
profiles
* also torsion around an axially free or non-compressible
guided torsional axis.
1972 Kollbrunner, C., Hajdin, N.: Dünnwandige Stäbe
(Thin-Walled Beams)
* an (erroneus) model of bimoment torsion of closed profiles
1975 Parland, H. : Lessons in structural mechanics in the
Department of Civil Engineering, Tampere
University of Technology
* a laterally guided case with one flexural and one torsional
degree of freedom for an L-profile
* transmission of bimoment quantities in some joints
1978 Roik, K: Dünnwandige Stäbe mit Zwangdrillachse,
* a case like before for a general open profile
* plane bending as a case of guided beams
1984 Yang Y.-B.: Linear and non-linear analysis of space
frames with non-uniform torsion
*transmission matrices of displacement and force
quantities in (some) joints, a special case
1986 Koivula, R: Avoprofiilisten sauvojen ohjattu vääntö
(Guided beams with open cross-section),
Rakenteiden mekaniikka 4/1986
* a general theory of guided beams with rigid open
cross-section
* the continuous restraints can prevent the deflection of an axis in one or two (all) directions, and axial elongation on one (non-compressible) axis.
* the transformation matrices between guided systems of axes and special points of open cross-sections.
1989 Schardt, R.: Verallgemeinerte Technische
Biegetheorie, VTB
* the general theory of the normal, flexural, torsional and distortional warpings of an open profile
* the Vlasov theory is a special case in Schardt´s theory
* the theory of Koivula 1986 can also be derived in terms of the generalized beam theory of Schardt, but not the theory of Kollbrunner and Hajdin 1972, without some further steps in the Schardt theory
1995 Kähönen, A, Niemi E.: Distortion of a double
symmetrical box section subjected to eccentric loading
- using beam on elastic foundation approach
* the approach is related to the theory of guided beams, because one warping is transformed to another in order to get the beam
solved. But until then no one had introduced any guided beam case with more than one non-compressible axes
1998 Koivula, R.: “Transformations of Force and Displacement
Quantities between Different Systems of Axes and Special
Points”, Research and Development; Proceedings of the 2nd
International Conference of Thin Walled Structures, Singapore,
ISBN 0-08-043003-1
2000 Koivula, R.: “Analysis of distortion of a thin-walled rectangle
beam using the theory of guided Vlasov beams.”
Proceedings of VII Finnish Mechanical Days, 2000.
* guided beams with more than one non-compresible axes
* a shear deformation as a degree of freedom of a Vlasov beam
* the introduced model is allowable, but not “exact” for the box
beam quadrant
* a link between the theories of open and closed cross-sections
2003. Koivula, R. : “Derivation of the Kollbrunner-Hajdin Theory of
the Thin-Walled Rectangular Box Beam under Torsion by
Dividing the Beam into Guided Vlasov beams with Open Cross-
Section.” Proceedings of the VIII Finnish Mechanical Days,
Espoo, ISBN 951-22-6569-9
* the two torsional axes of the half-box
* a little erroneous interpretetation of the Kollbrunner-Hajdin equation
2004. Koivula, R.: “A Thin-Walled Rectangular Box Beam under
Torsion: a Comparison of the Kollbrunner-Hajdin Solution
with a Solution by Dividing the Beam into two Guided Vlasov
Beams with open Cross-Section”
Proceedings of the 4th International Conference of Thin Walled
Structures, Loughborough, United Kingdom
AVOPROFIILISEN SAUVAN OHJATTU VÄÄNTÖ
Risto Koivula
Rakenteiden mekaniikkaikka, Vol. 18
No . 4 1985, s . 57 ... 94
TIIVISTELMÄ:
Ns. vapaasti deformoituvan sauvan muodonmuutostila voidaan esittää tyhjentävästi neljän siirtymasuureen avulla, jotka ovat pitenema vz, vääntöakselin taipumat vx ja vy sekä vääntökulma θ. Vääntöakseli yhtyy leikkausakseliin ja ns. pitenemäakseli painopisteakseliin.
Ohjatusti deformoituvalla sauvalla puolestaan liikemahdollisuuksia on rajoitettu sauvan pituudella vaikuttavin, yhden tai useamman pitkittäis- tai poikittaissuuntaisen vapausasteen poistavin tuennoin. Tästä johtuen on erotettava toisistaan toisaalta painopisteakselin ja pite-nemäakselin, toisaalta leikkausakselin ja vääntöakselin käsitteet. Kuormituksen ja normaali-voiman, taivutusmornenttien ja bimomentin väliset yhtälöt asetetaan sellaisessa koordinaa-tistossa, jossa nollapiste sijaitsee pitenemäakselilla ja sektoriaalinen napa vääntöakselilla. Tyhjentävän ratkaisun saamiseksi ohjatun väännön probleemalle tuennoissa vaikuttavine lii-tosvoimineen on tämän koordinaatiston mukaisin poikkileikkausarvoin lasketut leikkaus - ja modonmuutossuureet usein vielä muunnettava tavalliseen koordinaatistoon, jossa nollapiste on painopisteessä ja sektoriaalinen napa leikkauskeskiössa. Muunnokset voidaan usein suorittaa tässä kirjoituksessa esitetyin matriisein.
JOHDANTO
Seuraavan kirjoituksen tarkoituksena on valaista lähinnä teräsrakentamisen tarpeita silmällä pitäen ohjatun väännön teoriaa ja johtaa laskentakaavat ohjatun väännön avulla eräille tavan-omaisille rakenteille erityisesti alan kirjallisuudessa vähän käsitellyn ns. kahden vapausasteen systeemin osalta. Kahden vapausasteen systeemia on aiemmin kasitelty mm. lähteessä /2/.
Kaavat on pyritty johtamaan mahdollisimman yleisessä muodossa, jossa ohjatun väännön eräät tunnetut perustapaukset saadaan yhden yleisemmän teorian erityistapauksina ja jota teoriaa voidaan tässä kirjoituksessa käsiteltyjen perustapausten lisäksi käyttää esimerkiksi sellaisissa tapauksissa, joissa tuennasta aiheutuu sauvalle myos pituussuuntaisia kuormia, tai sellaisissa tapauksissa, joissa sauvaan kohdistuu pakkomuodonmuutoskuormia.
57
On kehitetty sellainen matriisimuotoinen esitystapa, jolla ohjatun väännön probleemoiden ohjelmointi tietokoneelle on mahdollisimman yleisessä muodossa mahdollisimman helppoa.
Osoittautuu, etta sauvan poikkileikkausarvot, sektoriaalinen koordinaatti, ym. suureet ohja-tussa väännössä voidaan yleensä lausua ohjaamattoman väännon vastaavien suureiden avulla ja näin siis palauttaa ohjatun vaannon tapaukset ohjaamattoman väännön käsitteisiin. On silti olemassa koko joukko rakenteita, nimenomaan silloin,jos ohjatun väännön yhteydessä joudu- taan tarkastelemaan esimerkiksi vääntöä vastustavaa jousituentaa tai kosketusprobleemoita, jolloin fysikaalisesti oikea kuva rakenteen toiminnasta voidaan saavuttaa ainoastaan ohjatun väännön avulla.Valitettavasti joukko käytännössä tärkeitä tapauksia, kuten voimakkaasti joustavat tuennat, menee myös ohjatun vaannon patevyysalueen ulkopuolelle.
Lähteessä /3/ esitetyssä Vlasovin teorialle perustuvassa johdossa väännöstä aiheutuvan nor-maalijännitysjakautuman verrannollisuudelle sektoriaaliseen koordinaattiin olen korvannut lähtöhypoteesin τzs = 0 profiilin keskiviivalla lähtöhypoteesilla τzr = 0, jossa r on profiilin seinämän keskiviivaan sidottua kaarikoordinaattia s vastaan kohtisuora koordinaatti. Lopputulokseen lähtöhypoteesin vaihtaminen ei vaikuta.
[RK: Lähtöhypoteesin vaihtaminen on tässä sikäli virheellinen, sillä fysikaalisesti tutkittavat asiat seuraavat nimenomaan edellisestä, alkuperäisestä hypoteesistä. Asia korjataan seuraavissa artkkeleissani.]
Käytettäessä poikittaissuunnassa tuetun sauvan ohjatun väännön kahden vapausasteen tapausta käytännön rakenteiden mitoituksessa on syytä muistaa, etta eräisiin stabiliteettikysy-myksiin tarvitaan lisätutkimusta. Tällaisia stabiliteettikysymyksiä ovat mm. kiepahdus vään-nön alaisena, ohjattu kiepahdus ja se,että vääntökulman kasvaessa suureksi kahden vapausas- teen systeemi saattaa eräillä profiileilla muuttua epävarmalle puolelle epälineaariseksi siten, että profiilin kiertyessä vääntöakseli käyristyy poispain kuorman läpimenopisteestä.
Terminologiassa on noudatettu lähteen /3/ linjaa, kuitenkin siten, että sana "kiertyminen" joh-dannaisineen on pyritty karsimaan pois, ja sana "vääntokeskiö" on korvattu sanalla "vääntö-napa". Sellaisista uusista nimityksistä kuten neutraalipiste ja pitenemäakseli on vastuussa kirjoittaja.
Ohjattua vääntoa pidetään usein aiheettomasti monimutkaisena tai vaikeana teoriana. Laskut ovat yleensä sitä yksinkertaisempia, mitä vähemmän sauvalla on vapausasteita. Kirjoitus on rajattu siten, että esimerkiksi sektoriaalisen koordinaatin määräämistä tai johdettujen diffrentiaaliyhtälöiden ratkaisuja ei käsitella, koska menetelmät ovat samanlaisia kuin ohjaamattomassakin väännössa ja siten kaikille lukijoille tuttuja.
58
1. LÄHTÖOLETTAMUKSET, SIIRTYMÄTILA
Lahtokohdaksi otetaan suora ohutseinainen, avoprofiilinen sauva, jolle seuraavat olettamukset voidaan katsoa olevan voimassa:
1) Poikkileikkaus ei vääristy, eli distortio wx = wy = 0 (1.1)
2) Lommahdusta ei sallita, eli profiilin seinaman voidaan katsoa toimivan levytilassa
3) Kaikkien leikkausjannitysten voidaan katsoa olevan profiilin seinaman keskiviivan suuntaisia, jolloin τzr = 0 profiilin koko alueessa (1.2)
4) Väännöttömässä taivutuksessa poikkileikkaus pysyy tasona (Bernoullin hypoteesi)
5) Leikkausmuodonmuutoksen γzs = τzs/G vaikutus sauvan siirtymiin katsotaan pieneksi
59
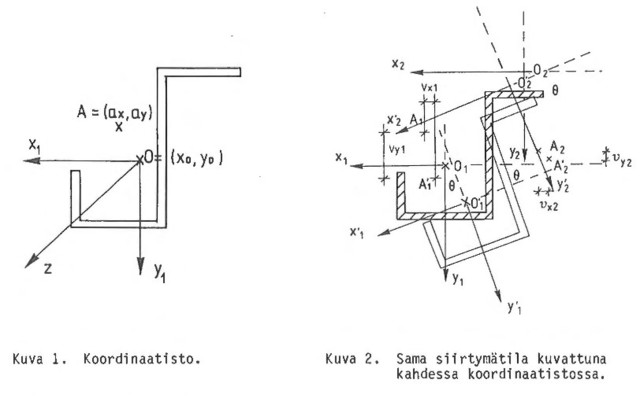
Poikkileikkauksen siirtymätila tasossa voidaan nyt kuvata seuraavilla yhtä1öi11ä:
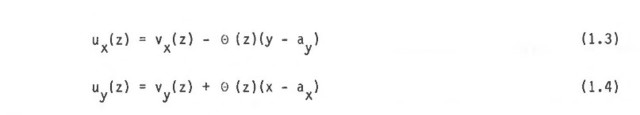
Tässä yhtälöryhmässä vx(z) ja vy(z) merkitsevät akselin A = (ax, ay) x- ja y-suuntaisia siirymiä ("taipumia") ja θ(z) on vääntökulma. Kiertymisen katsotaan tapahtuneen pisteen A ympäri.
Poikkileikkauksen siirtymätila voidaan lausua mielivaltaisessa järjestelmässä o1, A1, jossa o1 on järjestelmälle asetettu nollapiste ja A1 on sille asetettu sektoriaalinen napa.
Kuvassa 2 on esitetty sama siirtymatila kahdessa mielivaltaisessa, akseleiltaan yhdensuun-taisessa järjestelmässä O1,A1 ja O2 , A2. Siirtyneet akselit ja vastinpisteet on merkitty yläin- deksilla pilkku (') . Huomaa huomattavat erot "taipumien" vx1 ja vx2 sekä vy1 ja vy2 välillä. Vääntökulma θ(z) on tietenkin koordinaatistosta riippumaton.
60
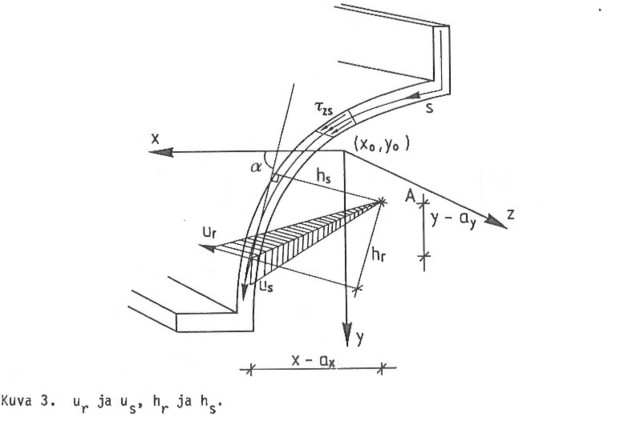
Johdetaan seuraavassa z-suuntaisen siirtyman uz lauseke lahtöolettamusta 3) lähtökohtana pitaen. Poikkileikkauksella olevan pisteen x(s,r), y(s,r) siirtymat x,y-koordinaatistossa olkoot ux ja uy. Vastaavat siirtymat koordinaatistossa s,r ovat talloin, huomioiden kaavat 1.3 ja 1.4.


61
Kaavoista 1.8, 1.9.1 ja 1.9.2 seka siita, etta x(s,r) ja y(s,r) ovat lahtohypoteesien 1), 4) ja 5) mukaisia jatkuvia funktioita kaikilla s:n ja r:n arvoilla, seuraa



62
2. TAIVUTUSMOMENTTIEN, BIMOMENTIN JA N0RMAALIVOIMAN VÄLINEN YHTEYS, LEIKKAUSSUUREIDEN N, My, Mx ja B RIIPPUVUUS VALITUSTA KOORDINAATISTOSTA
Kun yhtalöt 1.15 kerrotaan vuoron perään perusfunktioilla 1, -(x - xo), y - yo, ω(xo, yo, ax, ay, ωo) ja integroidaan yli profiilin pinta-alan A, saadaan leikkaussuureille seuraavat lausekkeet:
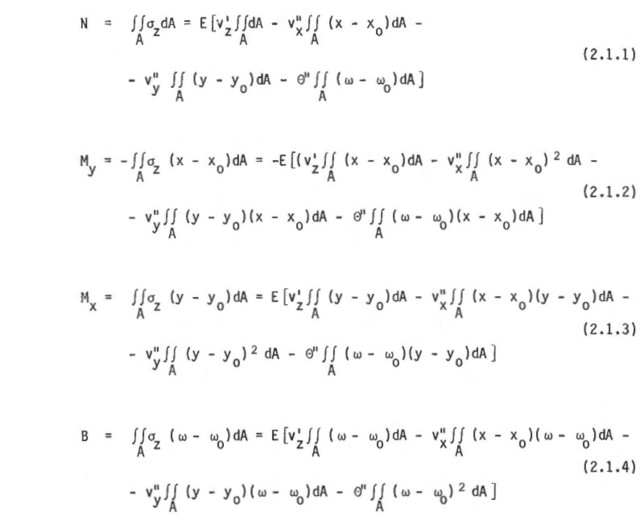
63
Kaavoissa 2.1.1 - 2.1.4 esiintyville pinta-alaintegraaleille ovat vakiintuneet käytäntöön seuraavat merkinnät:

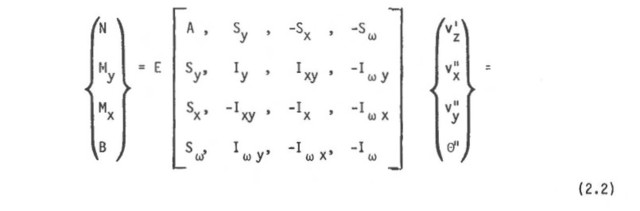
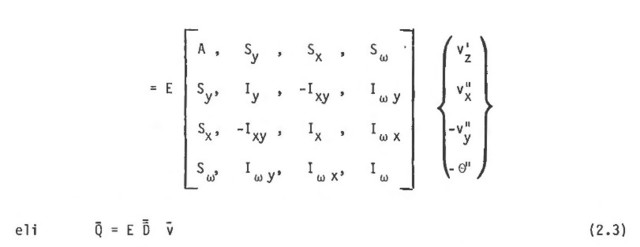
64
Koska sektoriaaliseksi navaksi (ax, ay) voidaan valita mielivaltainen poikkileikkaustason piste, koska nollapisteen koordinaatit xo ja yo ja sektoriaalisen koordinaatin vakiotermi ωo esiintyvät kaavaa 1.15 johdettaessa valinnaisten integroimisvakioiden ominaisuudessa ja koska näiden lisäksi myös koordinaatiston suuntakulma ϕ on valinnainen, ovat matriisin D alkiot riippuvaisia kaikkiaan kuuden eri koordinaatistovakion valinnasta,mikä on sama määrä kuin matriisissa D on lävistajan ulkopuolisia ns.kytkentätermejä. Tämä antaa mahdollisuuden valita sektoriaalinen napa A = (ax, ay), nollapiste O = (xo, yo), ωo ja suuntakulma ϕ siten, että vektoreiden Q ja v alkiot ovat keskenään toisistaan riippumattomia ja niiden aiheuttamat normaalijännitysjakautumat keskenään ortogonaalisia.
Matriisin D "siivoaminen" ortogonaalisuuden esteenä kulloinkin olevista kytkentätermeistä valitsemalla oikea koordinaattijärjestelmä,joka riippuu sekä profiilista että tuennasta sauvan pituudella, on paitsi mahdollista, yleensa myös välttämätöntä, jotta voitaisiin asettaa oikein kuormituksen ja leikkaussuureiden N, My, Mx ja B väliset yhtälöt.
Yleisessa tapauksessa leikkaussuureet N,My, Mx ja B ovat valitusta koordinaatistosta riip-puvia suureita.Kun vakiot xo ja yo valitaan siten,että staattiset momentit Sx = Sy = 0, niin xo ja yo ovat tälloin poikkileikkauksen painopisteen koordinaatit. Painopisteiden uraa sauvalla nimitetaan painopisteakseliksi. Seuraavassa "absoluuttisen" x,y-koordinaatiston origo sijoitetaan painopisteeseen, jolloin painopisteella xo = yo = 0.
Kun origon ollessa painopisteessa sektoriaalisen navan koordinaatit axo ja ayo valitaan siten, että sektoriaaliset keskipakoismomentit Iωx = Iωy = 0,niin axo ja ayo ovat poikkileikkauk- sen leikkauskeskiön koordinaatit. Leikkauskeskioiden uraa sauvalla nimitetään leikkausak- seliksi. Nimitys johtuu siitä, että väännöttömässä taivutuksessa leikkausjännitysten resultantti poikkileikkauksella kulkee aina leikkauskeskion kautta (osoitettu lähteessä /3/).
65

66
Leikkaussuurevektori Q koordinaatti akseleiden suunnaltaan mielivaltaisessa painopiste-leikkauskeskiö-koordinaatistossa voidaan siis aina esittaa vastaavanlaisessa paaakselikoordinaatistossa I;,TJ lasketun matriisin Do avulla seuraavana matriisiyhtalona:
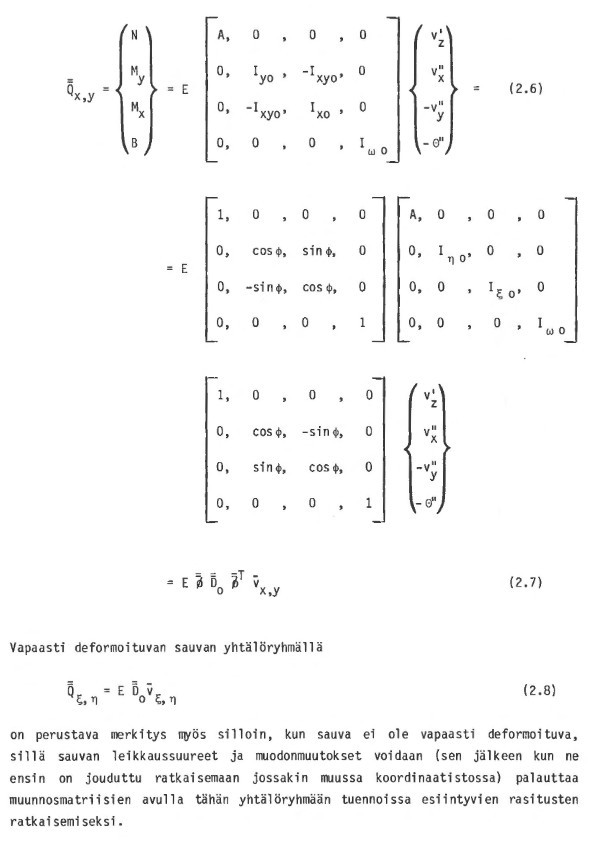
67
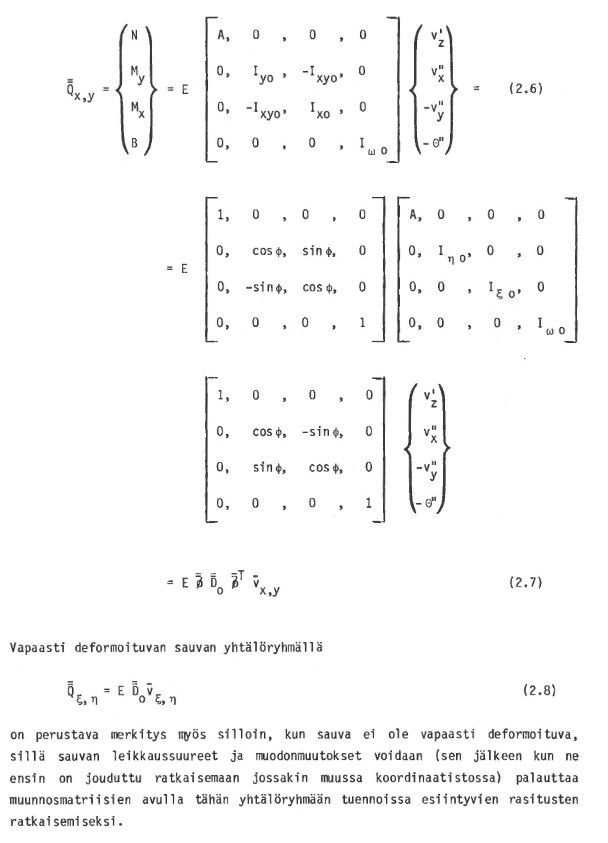
68

69


71

72
73
74

75

76

77

78
Ohjatun vaannon teoria patee silloin, jos on olemassa maaritelman edellytykset täyttävät pi-tenemäakseli ja vaantoakseli. Voidaan helposti konstruoida yksinkertaisiakin tuentoja, joissa jompaa kumpaa ei ole olemassa. Tällöin tässä esitetty teoria ei pade. Usein myös jompikumpi akseleista on epamääräinen, toisin sanoen rakenne esimerkiksi taipuu vääntymättä minkä tahansa akselin kautta kuormitettaessa, tai vääntöakseli ei taivu z-suuntaisista kuormista. Tällöin voidaan yleensä nollapiste tai sektoriaalinen napa sijoittaa mihin tahansa vaaditut edellytykset täyttävään pisteeseen, ja laskut johtavat samaan jannitysjakautumaan .
Periaatteena siis on, etta sauvan muodonmuutosten yhtalot asetetaan neutraalipiste-vääntö-napa-koordinaatistossa, jossa ratkaistut leikkaussuureet ja muodonmuutokset on usein vielä muunnettava painopiste-leikkauskeskiöjärjestelmään tukireaktioiden laskemiseksi.
SAUVAT, JOIDEN TUENTA EI OTA VASTAAN Z-SUUNTAISIA LEIKKAUSVOI-MIA JA JOIDEN MAHDOLLISET Z-SUUNTAISET KUORt4AT VOIDAAN KATSOA KOHDISTUVAN TUTKITTAVAN ALUEEN PÄIHIN
Rajataan nyt tarkastelu koskemaan yksinomaan otsikossa mainitun tyyppisia sauvoja, joita useimmat palkki-, orsi- ym. sauvarakenteet ovat. Niille on ominaista, että normaalivoima on taivutus- ja vääntömomenteista riippumaton, jolloin nollapiste x0,y0 kannattaa aina sijoittaa profiilin painopisteeseen.
Edella esitetty yleinen teoria yksinkertaistuu merkittavasti:

79
- Koordinaattijärjestelmien välinen muunnosmatriisi

80
Peruskaavat 2.38 voidaan nyt, ottaen huomioon kaavat 2.6, kirjoittaa muotoon

81
Yhtälö 4 .8 voidaan esittää myös käänteisessä muodossa

Lähteessä/3/ on todistettu,että väännöttömässä taivutuksessa tämän kohdan 4) mukaisilla sau- voilla leikkausvoimien resultantti kulkee aina leikkauskeskiön kautta.Voidaan osoittaa myös, että väännöttömässä taivutuksessa tämän luvun mukaisilla sauvoilla leikkausvoimien resul-tantti kulkee aina vääntöakselin kautta. Jos siis vääntoakseli ja leikkausakseli ovat eri paikas-sa,niin joko väännöttömässä taivutustilassa 1eikkausvoimien resultantti suuntautuu vääntöna-vasta leikkausnapaan tai väännötön taivutus ei ole mahdollinen. Tästä seuraa kaavan 4.7.5 ehto.
82
POIKKILEIKKAUKSELTAAN VÄÄRITYMÄTTÖMÄN, POIKITTAISSUUNNASSA ERI TAVOIN TUETUN SAUVAN PERUSTAPAUKSIA
Seuraavassa esityksessä sellaiset voimasuureet jotka ovat tuntemattomia,ts.niitä ei voida las-kea suoraan kuormituksesta, on merkitty yläindeksilla kysymysmerkki (?) . Sellaiset siirtyäat puolestaan, jotka ovat tunnettuja, ts. annetaan lähtötietona, ovat näissä esimerkeissä aina nol-lan suuruisia. Sellaiset leikkaussuureet, muodonmuutokset ja poikkileikkausarvot, jotka poik-keavat painopiste-leikkauskeskiojärjestelmän vastaavista suureista, on merkitty alaindeksillä yksi (1).
Tapaus 1. Vapaasti deformoituva sauva, kolme vapausastetta
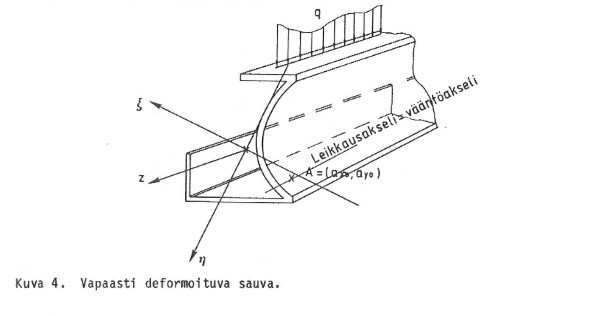
Kuormitus q on edullisinta jakaa pääakselien suuntaisiin komponentteihin, joiden kuvitellaan vaikuttavan leikkausakselilla, joka tunnetusti on tässä tapauksessa myös vääntöakseli, sekä vääntökuormaan m, joka on suuruudeltaan q x a, jossa a on kuormitusresultantin lyhin etäisyys leikkausakselista kussakin poikkileikkauksessa.
83

Jos taas rakenteeseen liittyy taipumaa vastustava jousituenta, voidaan sauva laskea kimmoi-sella alustana olevana palkkina ainoastaan silloin, jos jouset kiinnittyvät profiiliin leikkaus-akselin kohdalla ja vaantokuorma m = 0.Muussa tapauksessa analyysi johtaa monimutkaisiin yhtälöryhmiin.
84
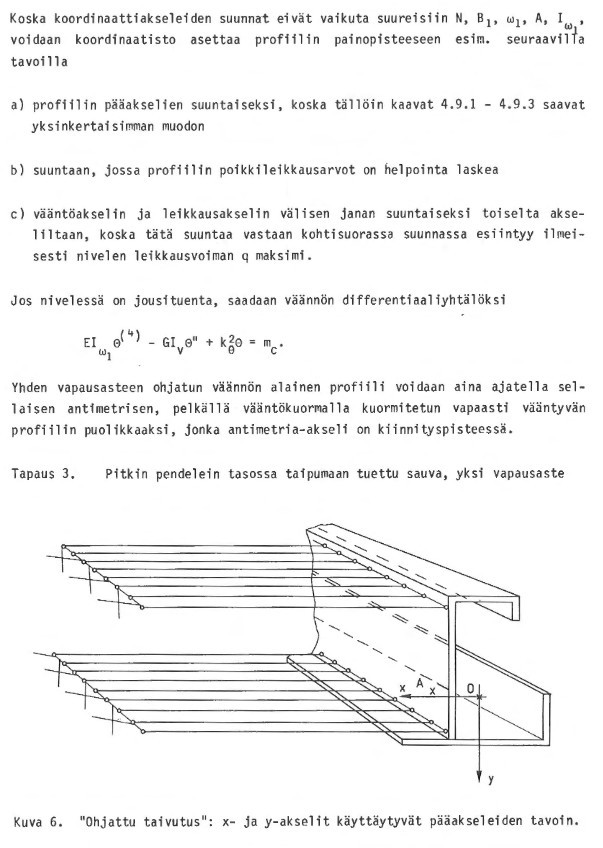
Tapaus 2. Sauva on tuettu pituussuuntaisella, pituussuuntaisia leikkausvoimia vastaanottamattomalla nivelella jäykkään alustaan, yksi vapausaste
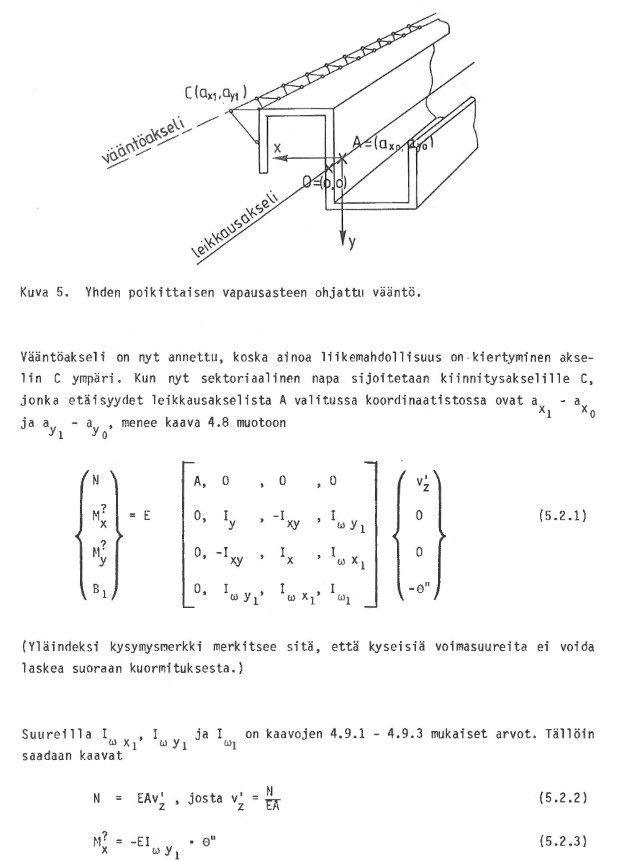
85

86
87

88
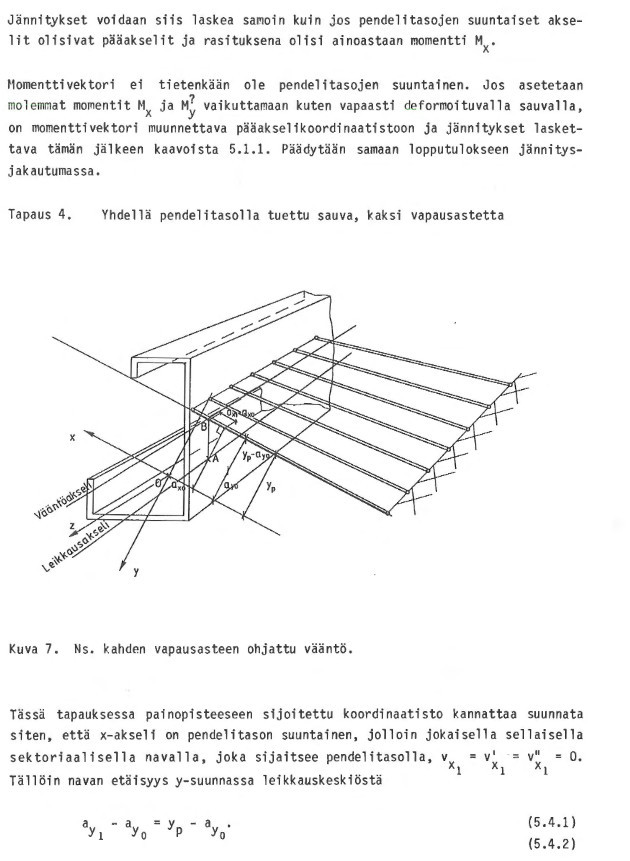
89

90
91
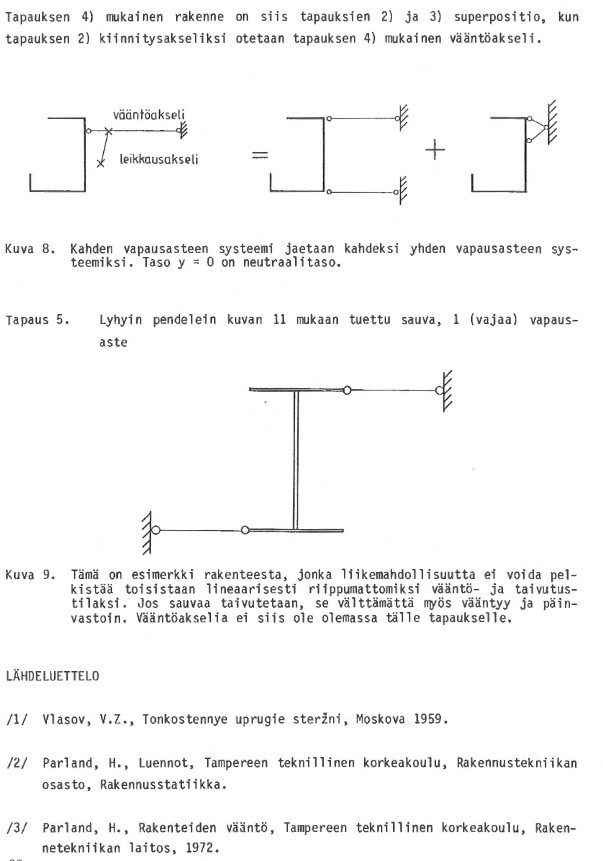









ERILAISTEN AVOPROFIILIEN JATKUVASSA PÄITTÄISLllTOKSESSA
Nro 1, 1997, s. 25-46
Risto Koivula
Tiivistelmä
Kirjoituksessa mallinnetaan poikkileikkaukseltaan kolmesta suorakulmaisesti liittyvästä kais-tasta (laipoista ja uumasta) muodostuvan avoprofiilisen 14 -vapausasteisen palkkielementin siirtymä- ja voimasuureiden välittyminen ns. off-set-paittaisliitoksessa, jossa liittyvät profiilit ovat keskenään erilaisia tai ne on liitetty toisiinsa epäkeskeisesti.Jatkuvuus merkitsee sitä,että mitään vapausastetta ei ole niveloity tai muuten vapautettu.Liitos on suora,ja molempien pro- fiilien kaistat ovat akseleiden y ja z suuntaisia, mutta teoria voidaan yleistää kulma-, haara- ym. liitoksille.
Johdanto
Kirjallisuudessa on useissa lähteissä esitetty estetyn väännön huomioon ottava avoprofiilinen palkkielementti /2/,/8/.Myös vinoutumisvapausasteita huomioon ottavia palkkielementtejä on kehitelty /9/, /10/. Avoprofiilisille elementeille lukuun ottamatta kaksois- ja pistesymmetrisiä profiileita on ominaista, että niiden painopiste-, leikkaus- ja kiertymäakselit eivät yhtene. Oh-jatusti deformoituvilla sauvoilla efektiiviset erikoisakselit riippuvat myös tuennasta. Tästä seuraa, että ns.keskeiset liitokset,joissa solmu voidaan ajatella yhdeksi, kahdeksi tai kolmeksi pisteeksi, joissa liittyvien elementtien toisiaan vastaavat erikoisakselit kohtaavat jatkuvin muodonmuutoksin, ovat avoprofiileilla poikkeus ja epäkeskeiset (muut) saantö.
Liitosten epäkeskeisyyden vaikutuksen koko rakenteen voimasuurejakautumaan huomioon ottavan palkkirakenteiden elementtimenetelmiin rungon on kehittänyt Timo Bjork liihteissii /2/ ja /6/.
25
1) Sauvaelementit deformoituvat avoprofiilisen ohutseiniimiiisen poikkileikkaukseltaan vinoutumattoman sauvan teorian mukaisesti, vapaasti tai ohjatusti.
2) Elementit on kiinnitetty toisiinsa poikittaisen levyn viilityksellä. Tiimiin levyn liikemah-dollisuudet ovat solmusiirtymiä. Siirtymävapausasteita otetaan tiissii tapauksessa huomioon 7 kappaletta:
- pitenemii (etenemä) u , solmulla siirtymä U
- taipumat v ja w, solmulla siirtymät V ja W
- kiettymät (taipuman detivaatat) θv = - dw/dx ja θw = dv/dx, solmulla Θv ja Θw
- vääntökulma θu, solmulla Θu
- vääntymä (vääntokulman derivaatta) θ´u, solmulla Θ'u
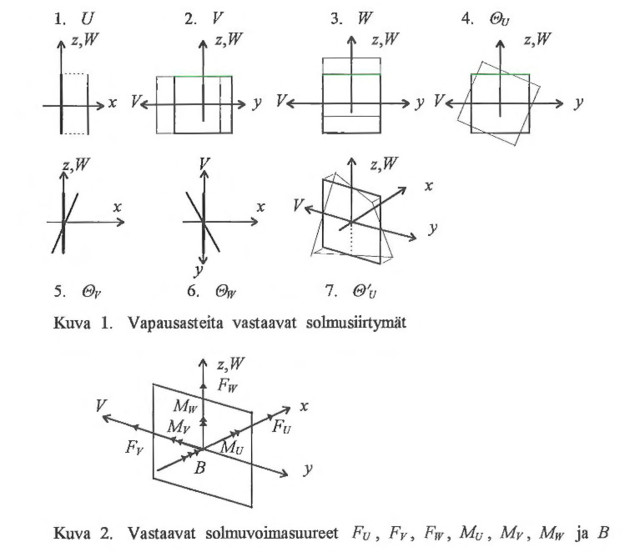
4) Vapausastetta Θ'u vastaava solmudeplanaatiomuoto (kuva 1.7.) on
Ω = -yz (1)
5) Liitoslevyn vääntöjäykkyyden GIt katsotaan olevan pieni verrattuna profiilin kaistojen tai-vutusjäykkyyksiin keskipisteensä ympäri vahvemmassa suunnassa,mutta sen laattataivutus-jäykkyyden katsotaan olevan suuri venattuna kaistojen laattataivutusjäykkyyksiin keskivii-vansa suhteen. Tämä vastaa tilannetta, jolloin kaistat liittyvät liitoslevyyn sarananivelin. Pro-fiilin seinämä ei ota vastaan seinämän keskiviivan suuntaisia pistemomentteja. Tutkimme siis toistaiseksi vain kuvan 3. tapausta 1).
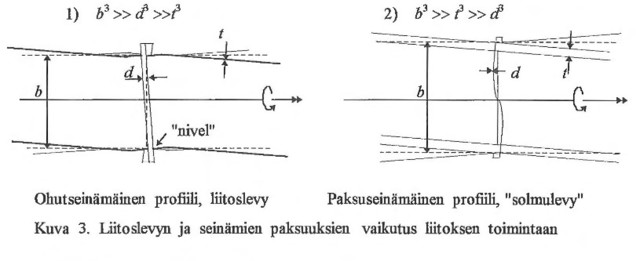
Ohutseiniimiiisen poikkileikkauksen yleistetty sektriaalinen koordinaatti Ωi(yi, zi) on lokaali siirtymäsuure, joka fysikaalisesti merkitsee sauvan päähän kiinnitetyn poikittaisen laatan, johon profiilin kaistat liittyvät sarananivelin keskiviivaltaan, (laatta)taipumaa ui(yi, zi), kun sauvassa vastaavalla kohdalla vaikuttaa vääntymä (vääntökulman derivaatta) Θ'u(x) = 1 . Poikkileikkauksen keskiviivalla yleistetty sektoriaalinen koordinaatti yhtenee "tavallisen" sektoriaalisen koordinaatin kanssa:

levyn tasossa bimomentin





Miinusmerkki johtuu vasenkatisesta koordinaatistosta. Kaavat 17 ja 18 antavat seinamää vas-taan kohtisuoran pistemomentin vaikutukselle saman tuloksen.Sen sijaan laipalle keskiviivan suunnassa vaikuttavan pistemomentin tapauksessa syntyy itseisatvoltaan 2Mc suuruinen ero, jossa c on vaikutuspisteen etäisyys uumasta. Koska seiniämiin ei katsota ottavan laattana vas-taan momenttikuormaa (oletus 5),liitoslevy siirtää momentin kaksitukisena palkkina laippojen normaalijännityksiksi.
Kaava 18 ei päde seinämiin keskiviivan ulkopuolella vaikuttavalle pistemomentille.
32






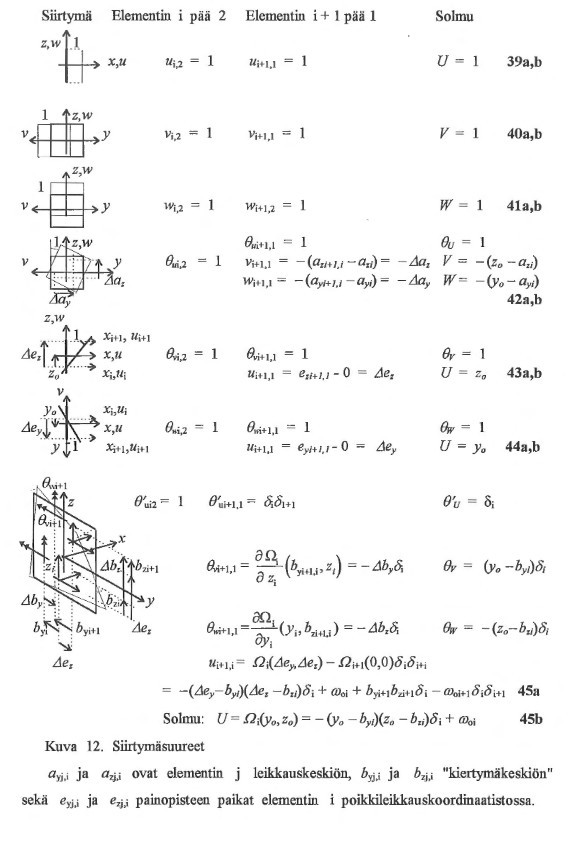


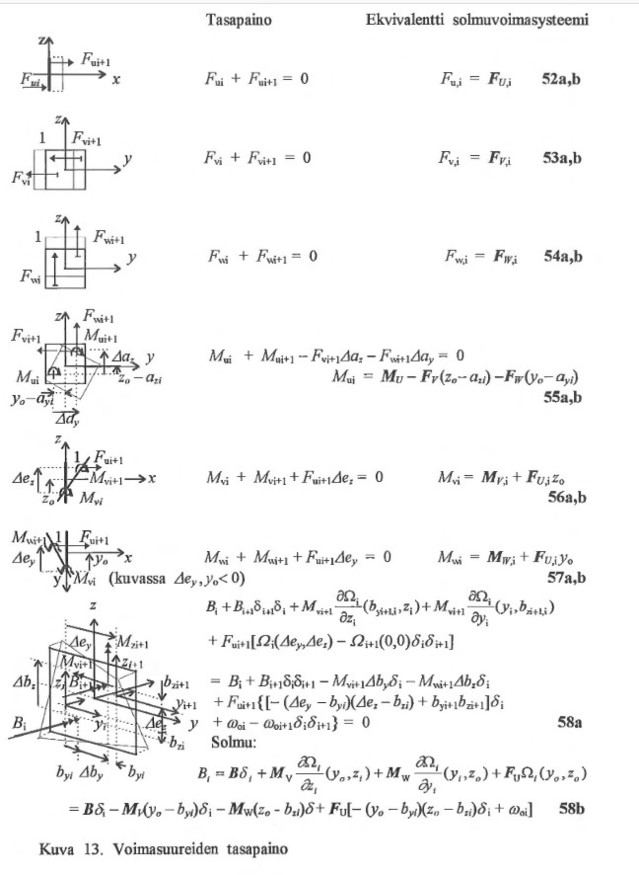
Annetaan sauvan piiiille 2 kullekin voimasuureelle vastaava virtuaalinen siirtymä suuruudel-taan 1, ja asetetaan kaikkien voimasuureiden näissä siirtymissä tekemä virtuaalinen työ nollaksi.
41






A THIN-WALLED RECTANGULAR BOX BEAM UNDER TORSION:
A COMPARISON OF THE KOLLBRUNNER-HAJDIN SOLUTION WITH A SOLUTION BY DIVIDING THE BEAM INTO TWO GUIDED VLASOV BEAMS WITH OPEN CROSS-SECTION





THE GUIDED SYSTEM OF AXES AND SPECIAL POINTS FOR THE HALF PROFILE
The beam is divided into two guided Vlasov beams with a U cross-section along one of the two planes of symmetry of the beam. The part beams are U profiles which are guided by non-compressible axes along the edges of the “flanges”, in other words along the mid-lines of the box sides. These edges of “flanges” are guided also by lateral restraints in the cutting plane to keep the distance from the original box centre (C), around which the half box so is guided to rotate. Figure 2.


In the beginning two independent degrees of freedom must be regarded for the U profile with the non-compressible axes along the edges, but without the lateral support:
First, caused by the normal stresses given rise by the bimoment warping, the cross-section tends to rotate around a sectorial pole, around which it is possible to draw a sectorial area with zero value at the non-compressible axes. This guided sectorial pole (D) is placed on the symmetry axis of the U cross-section at the “flange” length distant from the web behind the web (outside the box).Deformed by the warping nor- mal stresses only the cross-section rotates around this guided torsional axis. Loa-ding that beam through this axis in w-direction does not give rise to normal stresses.
Second, for cases of guided beams with two non-compressible axes,the shear defor- mation from the constant shear flow between these axes must be taken into consi-deration as an independent degree of freedom. Caused by the constant shear flow deformation, this axially guided along the flange edges, but laterally non-guided U cross section tends to rotate around a St Venant torsional centre (B), which is placed at the intersectional point of the bisectors of the angles (at equal perpendicular distant from all three sides of the cross-section) if the wall thickness is constant. The cross-section rotates around the point B without any tendency to deplanation and normal stresses.
The lateral guiding, fixing the cross section to rotate around the box centre axis C, constitutes a coupling between these two for a laterally non-guided profile indepen-dent degrees of freedom.To match the deformations from the warping torsion around D and the twisting torsion around B, we must match the translations of point (axis) C from these two degrees freedom of the cross-section to zero.
Like the moment is separated into warping and twisting moments, also the shear force must be separated into two components, one placed at the sectorial pole D and proportional to the StVenant twisting moment around B, and the other placed at the StVenant shear centre B and proportional to the warping moment (the derivative of the bimoment) around the sectorial pole D.





Kommentit